Analyzing Clinical Significance: The Statistical Approach

Introduction

The statistical approach to clinical significance evaluates whether a patient has moved from a dysfunctional (“clinical”) population to a functional (“non-clinical”) population as a result of an intervention. This method is based on the idea that a meaningful change involves not just a reduction in symptoms, but a transition to a state of healthy functioning.

To apply this method, we must first define the score distributions of both the clinical and functional populations. From these, we calculate a cutoff score that optimally separates the two groups. A patient is then considered to have made a clinically significant change if they were in the clinical range before treatment and in the functional range after treatment.

This vignette demonstrates how to use the cs_statistical() function to perform this analysis. It’s important to note that this method is a key component of the powerful Combined Approach, which is often the most informative way to assess clinical significance.

library(clinicalsignificance)

Defining Populations and Calculating a Cutoff

The most crucial step in this approach is defining the functional population. This requires obtaining summary statistics (mean and standard deviation) for the outcome measure from a relevant non-clinical or healthy sample.

For our example using the BDI-II from the claus_2020 dataset, we will use normative data from Kühner et al. (2007), who reported a mean of 7.69 and a standard deviation of 7.52 for a German non-clinical sample.

The clinicalsignificance package provides three methods for calculating the cutoff, specified by the cutoff_type argument: - "a": Based only on the clinical sample’s distribution. - "b": Based on the functional sample’s mean and the clinical sample’s standard deviation. - "c": (Recommended) Incorporates the mean and standard deviation from both the clinical and functional populations to find an optimal midway point. This is generally the most robust and objective choice.

Example Analysis

Let’s perform the analysis using the recommended cutoff type “c”. The function will automatically calculate the mean and standard deviation for the clinical sample from the claus_2020 pre-treatment data.

# Perform the statistical analysis
stat_results <- claus_2020 |>
  cs_statistical(
    id = id,
    time = time,
    outcome = bdi,
    pre = 1,
    post = 4,
    m_functional = 7.69,
    sd_functional = 7.52,
    cutoff_type = "c"
  )

summary(stat_results)
#> 
#> ---- Clinical Significance Results ----
#> 
#> Approach:     Statistical
#> Method:       JT
#> N (original): 43
#> N (used):     40
#> Percent used: 93.02%
#> Cutoff type:  c
#> Cutoff:       21.02
#> 
#> -- Cutoff Descriptives
#> 
#> M Clinical | SD Clinical | M Functional | SD Functional
#> -------------------------------------------------------
#> 35.48      |        8.16 |         7.69 |          7.52
#> 
#> 
#> -- Results
#> 
#> Category     |  N | Percent
#> ---------------------------
#> Improved     | 13 |  32.50%
#> Unchanged    | 27 |  67.50%
#> Deteriorated |  0 |   0.00%

The summary tells us that the calculated cutoff score is 21.6. Based on this, 32.5% of patients were classified as “Improved,” meaning they started above this cutoff (in the clinical range) and ended below it (in the functional range).

Visualizing the Results

The plot for the statistical approach is unique. It features two dashed lines representing the cutoff score on both the pre-treatment (x-axis) and post-treatment (y-axis). These lines divide the plot into four quadrants:

Top-Right: Clinical before and after (Unchanged).
Bottom-Left: Functional before and after (Unchanged).
Bottom-Right: Clinical before, functional after (Improved).
Top-Left: Functional before, clinical after (Deteriorated).

plot(stat_results)
#> Ignoring unknown labels:
#> • colour : "Group"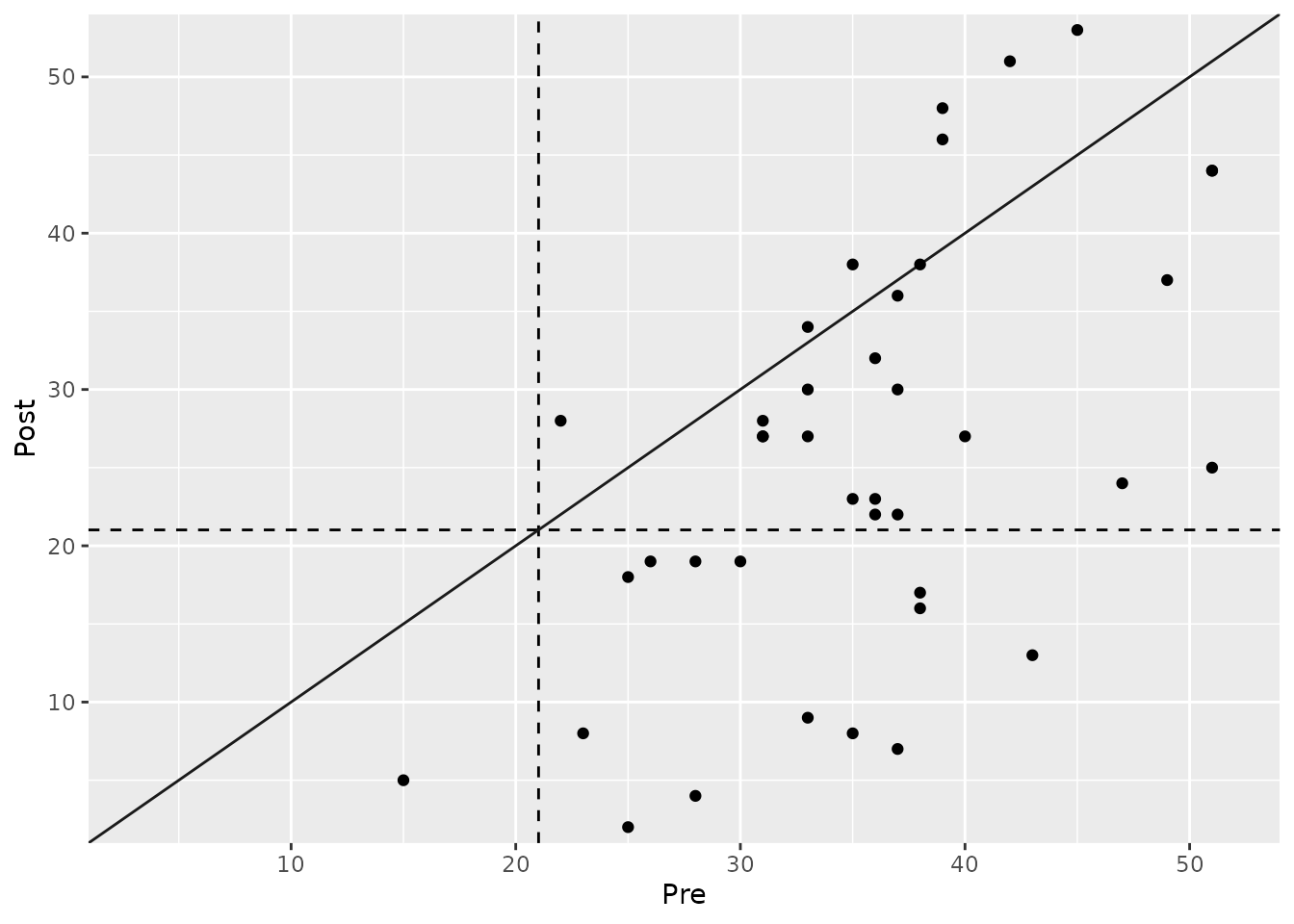

Grouped Analysis

We can also investigate if the proportion of patients who transitioned to the functional population differs between the treatment groups (TAU vs. PA).

# Grouped statistical analysis
stat_grouped <- claus_2020 |>
  cs_statistical(
    id = id,
    time = time,
    outcome = bdi,
    pre = 1,
    post = 4,
    m_functional = 7.69,
    sd_functional = 7.52,
    cutoff_type = "c",
    group = treatment
  )

summary(stat_grouped)
#> 
#> ---- Clinical Significance Results ----
#> 
#> Approach:     Statistical
#> Method:       JT
#> N (original): 43
#> N (used):     40
#> Percent used: 93.02%
#> Cutoff type:  c
#> Cutoff:       21.02
#> 
#> -- Cutoff Descriptives
#> 
#> M Clinical | SD Clinical | M Functional | SD Functional
#> -------------------------------------------------------
#> 35.48      |        8.16 |         7.69 |          7.52
#> 
#> 
#> -- Results
#> 
#> Group |     Category |  N | Percent | Percent by Group
#> ------------------------------------------------------
#> TAU   |     Improved |  5 |  12.50% |           26.32%
#> TAU   |    Unchanged | 14 |  35.00% |           73.68%
#> TAU   | Deteriorated |  0 |   0.00% |            0.00%
#> PA    |     Improved |  8 |  20.00% |           38.10%
#> PA    |    Unchanged | 13 |  32.50% |           61.90%
#> PA    | Deteriorated |  0 |   0.00% |            0.00%

The analysis reveals a substantial difference: 47.6% of patients in the Placebo Amplification (PA) group moved into the functional range, compared to only 15.8% in the Treatment as Usual (TAU) group.

The plot makes this difference visually apparent:

plot(stat_grouped)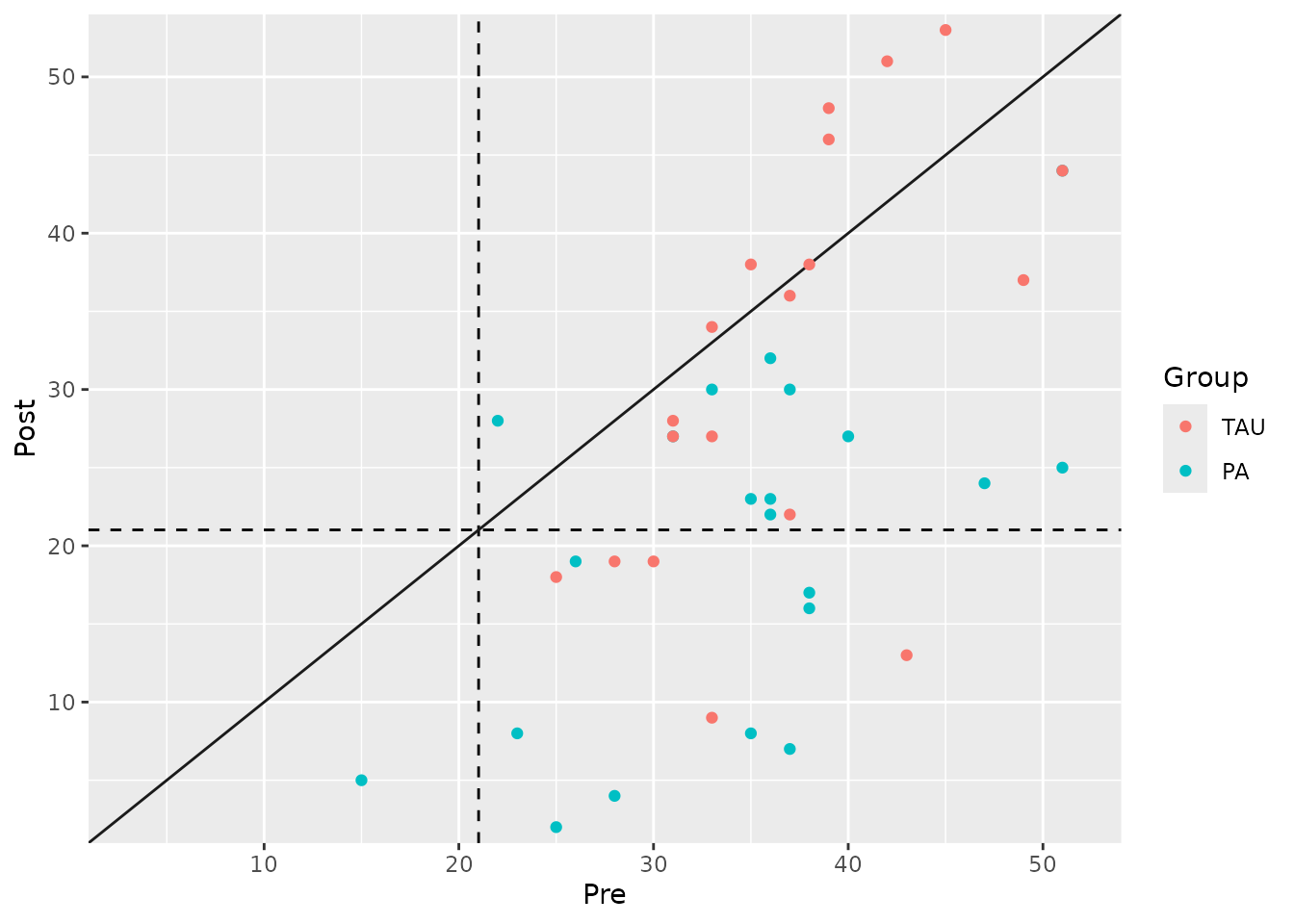

Summary and Next Steps

The statistical approach provides a powerful criterion for clinical significance by focusing on a patient’s end-state functioning.

Strength: It defines recovery in an absolute sense (return to normality) rather than just relative change.
Limitation: It requires reliable normative data for a functional population, which may not always be available. Also, it doesn’t consider the magnitude of change for patients who do not cross the cutoff.